Transducers Compose Top-to-Bottom

2019-01-22 by Tomas Tulka

Let's code some transducers and take a deeper look at how they work under the hood to see differences from pipes.

Transducers are composable reducers. A transducer takes a reducer and returns another reducer. Transducers compose via simple function composition. But, there is a tiny difference between function and transducer composition: functions compose bottom-to-top while transducers top-to-bottom.

Disclaimer: This text presumes basic knowledge of transducers and function composition.

Function Composition

First of all we discuss the basics: function composition.

Function composition is the process of chaining the output of a function to the input of another function. In algebra, composition of functions f and g means (f ⋅ g)(x) = f(g(x)).

In JavaScript we can write:

const inc = (x) => x + 1;
const double = (x) => x * 2;

const incAndDouble = (x) => double(inc(x)); // compound function

incAndDouble(2); // 6

Of course, we can do better! Let's create a general function compose:

const compose = (...fns) => x => fns.reduceRight((y, f) => f(y), x);

const incAndDouble2 = compose(double, inc);

incAndDouble2(2); // 6

As you can see, the functions are applied from bottom-to-top as in the definition (f ⋅ g)(x) = f(g(x)). It means, first g(x) is applied and, then, the output is used as the input for f(). If we want a composition applying from top-to-bottom, we can do it: this kind of composition is called a pipe:

const pipe = (...fns) => x => fns.reduce((y, f) => f(y), x);

const incAndDouble3 = pipe(inc, double);

incAndDouble3(2); // 6

Transducer Composition

Probably the most useful is the mapping transducer. Let's define it:

const map = f => step => (a, c) => step(a, f(c));

The map takes two curried parameters f and step. f is a mapping function and step is a reducer function to calculate (reduce) the result. We can peep at it with the following code:

const testReducer = map(double)((a, c) => console.log(c));
[1,2,3].reduce(testReducer, 0); // prints 2, 4, 6 into the console

Now we can use the composite function from above:

const incAndDouble4 = compose(map(inc), map(double));

const concat = (a, c) => a.concat([c]);

const incAndDoubleReducer = incAndDouble4(concat);

[1,2,3].reduce(incAndDoubleReducer, []); // 4, 6, 8

If you paid attention you maybe noticed one thing. Compare these two lines:

const incAndDouble2 = compose(double, inc);
const incAndDouble4 = compose(map(inc), map(double));

We didn't redefine the compose function, the result remains the same, but the order of functions for the composition is the other way around. How is this possible? Let's analyse it...

The composite function is pretty straight-forward: it takes a function from bottom-to-top, applies it (first to the init value x) and uses the output as the input for the next function. The difference between double and map(double) is, that map(double) returns a transducer function, not a scalar value as double does. This transducer function takes a parameter step, which is a reducer. It means, f(y) from the compose function is transducer(reducer); after evaluating it we get a step reducer function, which is then used as a new input y for the next transducer. Well, it means those two lines above define different kinds of function:

const incAndDouble2 = compose(double, inc);  // function (x) => x
const incAndDouble4 = compose(map(inc), map(double));  // transducer (reducer) => reducer

Composition uses reducing in the bottom-to-top direction (reduceRight), the result of the composition is the top-most transducer function which contains the next (to-bottom direction) transducer's result reducer (in the step parameter). This next reducer is applied after the current reduction (mapping) is applied.

We can write this particular composition function as:

const compose = (...reducers) => initReducer => reducers.reduceRight(
    (previousReducer, currectTransducer) => currectTransducer(previousReducer), initReducer);

Each reducer in the composition has a reference to the previous reducer (step). The final reduction starts with the top-most reducer which applies its functionality (mapping) and then executes the referenced reducer (step(...)). This brings the reducing in the opposite direction (top-to-bottom) from the transducers composition (bottom-to-top).

We can break down our example execution as following:

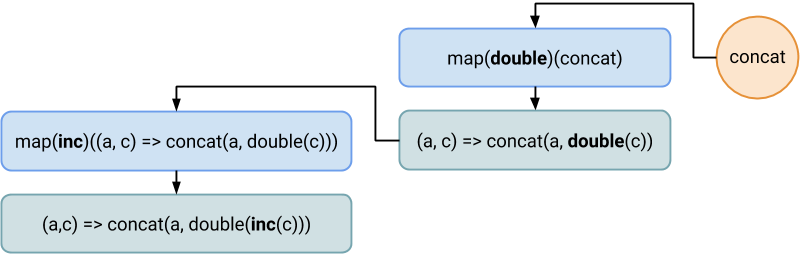
As we can see, the result reducer applies functions in order: inc, then double, then concat. As expected.

Neat.

Happy transducing!